由題意，Rt△ABC中，∠ACB=90°，∠BAC=60°，則∠ABC=30°。BC的垂直平分線DE交BC于D，AB于E，則EB=EC。延長DE至F，因?qū)ΨQ性，可得EF=ED，故F與C關(guān)于DE對稱，△ECF為等邊三角形。
-
-
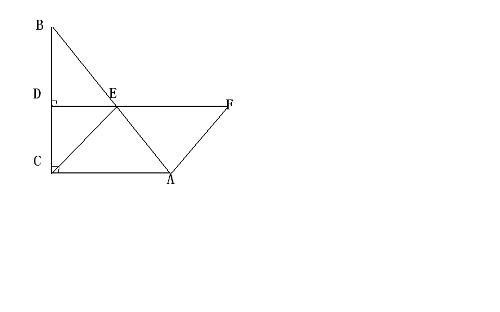解：在Rt△BDE中，
∠B＝30°，
∴∠BED＝60°，
∵DE為BC中垂線，
∴∠CED＝∠BED＝60°，
∴∠AEC＝180－2×60＝60°，
∵∠BAC＝60°，
∴△ACE為正△，
∴AF＝CE＝AE，
∵∠AEF＝∠BED＝60°，
∴△AEF為正△，
∴∠F＝∠ACE＝60°，∠CEF＝∠CAF＝120°，
∴四邊形ACEF為平行四邊形，
在△ACE中，
AC＝CE，
∴平行四邊形ACEF為菱形。 -
(1) ∵AC＝CB 又∵∠ACE＝∠CBD＝90° 又∵∠EAC＝∠DCB＝90°－∠ACF ∴△ACE≌△CBD ∴AE＝CD (2) ∵BD＝5cm ∴CE＝5cm ∴CB＝10cm ∴AC＝10cm
-
（解：在Rt△BDE中，
∠B＝30°，
∴∠BED＝60°，
∵DE為BC中垂線，
∴∠CED＝∠BED＝60°，
∴∠AEC＝180－2×60＝60°，
∵∠BAC＝60°，
∴△ACE為正△，
∴AF＝CE＝AE，
∵∠AEF＝∠BED＝60°，
∴△AEF為正△，）→雖然前面解的也不好但我還是得尊重下你但是后面也太爛了把
接下來我改的∴AE=AF=EF∵等邊△AEC
∴CA=CE=AE
即CA=CE=AE=EF
∴四邊形ACEF為菱形。→好好學(xué)數(shù)學(xué)把，沒學(xué)好就出來學(xué)人家混！
-
證明：∵∠ACE=90°，DE垂直平分BC， ∴DF∥AC，AE=CE， ∴∠B=∠BCE， ∵∠B+∠BAC=90°，∠ACE+∠BCE=90°， ∴∠BAC=∠ACE， ∴AE=CE=AE， ∵∠BAC=60°， ∴ΔACE是等邊三角形， ∴∠AEF=∠CAE=60°， ∵AF=CE=AE， ∴ΔAEF是等邊三角形， ∴EF=AE=AF=AC=CE， ∴四邊形ACEF是菱形。************************************************************************************ ^__^真心祝你學(xué)習(xí)進(jìn)步，如果你對這個答案有什么疑問，請追問， 另外如果你覺得我的回答對你有所幫助，請千萬別忘記采納喲！ 如果有其他問題，歡迎向我求助。與本題無關(guān)的就請不要追問了。 答題不易呀。懂了記得選滿意。 ************************************************************************************
-
證明：延長CE和BA交于F
∵BE平分∠ABC
∴∠CBE=∠FBE
∵BE=BE
BE⊥CF
∴△CBE全等于△FBE
∴CE=FE=CF/2
∵∠BAC=90°
∠BDA=∠CDE
∴∠ABD=∠ACE
∵AB=AC
∠BAC=∠CAF=90°
∴△BAD全等于△CAF
∴BD=CF
∴CE=BD/2
最新回答 更多>
相關(guān)問答
- 步步高9288t的basic腫么用
- gta5什么時間出來的
- 華為榮耀六plus,儲存卡裝在什么地方?
- 美版蘋果s4和國行的4 要哪個更好？ 美版4s比國行4貴了400
- 華為的運(yùn)動健康腫么同步微信運(yùn)動呢?
- 榮耀手表S1哪些功能需要華為穿戴在手機(jī)后臺運(yùn)行
- 我的微信運(yùn)動腫么看不到我的步數(shù)?
- 2011-T3鋁合金的性能好不好
- 國歷90年12月30日是什么星座
- gta5腫么關(guān)閉彈幕
- 20新款的東風(fēng)風(fēng)神ax7和長安cs78plus哪個更適于入手，三大件哪款強(qiáng)？
- 微信運(yùn)動腫么和手機(jī)同步步數(shù)?
- 為何我摁F4沒反應(yīng)呢，應(yīng)該說功能鍵都沒反應(yīng)，在開機(jī)時
- 諾基亞E5相機(jī)的聲音腫么關(guān)
- 佳明Vivoactive和佳明Vivoactive HR有什么不同